Seriler konu anlatımı video çözümlü soruları testi çöz izle indir
Herhangi bir (x
n) dizisinin sonlu tane elemanını değil de tüm elemanlarını "toplayalım". x
1+ x
2 + ... + x
n + ... "toplamına" seri denir.
Bir (x
n) dizisi verilsin. Bu dizinin ilk n tane teriminin toplamı olan x
1+ x
2 + ... + x
n ifadesi sembolik olarak gibi yazılır. Buradaki Σ (sigma) harfi bu tür toplamları kısa olarak yazmak için kullanılır. k ya toplama indisi denir ve k indisi yerine başka indisin kullanılması sonucu etkilemez.
Σ işareti matematikde çok kullanışlıdır ve çok zaman uzun ifadelerin yazılımını kısaltmaya imkan verir.
Şimdi (x
n) dizisinin sonlu tane elemanını değil de tüm elemanlarını "toplayalım". x
1+ x
2 + ... + x
n + ... sonsuz "toplamına" seri denir.
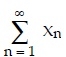
Sigma gösterimi yardımı ile bu seri gibi gösterilir. Şimdi sonsuz sayıda gerçel sayının toplamına anlam kazandırmak için
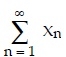
serisinden yeni (s
n) dizisini elde edelim:
s
1 = x
1 , s
2 = x
1+ x
2 , s
3 = x
1+ x
2 + x
3 , ... , s
n = x
1+ x
2 + ... + x
n , ...
Eğer (s
n) dizisi yakınsak olup limiti a ise
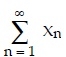
serisine yakınsak seri denir ve
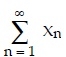
=a
gibi yazılır. a sayısına serinin toplamı da denilir.
Eğer (s
n) dizisi ıraksak ise
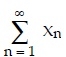
serisine ıraksak seri denir.
x
1 , x
2, ... sayılarına serinin terimleri, x
n ye genel terimi, (s
n) dizisine serinin kısmi toplamlar dizisi denir.
Görüldüğü gibi sonsuz sayıda gerçel sayının "toplamı", sonlu sayıdakilerin toplamlarının bir limiti olarak tanımlanmaktadır.
A. SERİLER
Tanım
|
(an) reel terimli bir dizi olmak üzere,
sonsuz toplamına seri denir.
an ye serinin genel terimi denir.
|
Tanım
|
Serinin ilk n teriminin toplamı olan,
ifadesine serinin n. kismî toplamı denir.
dizisine serinin kısmî toplamlar dizisi denir.
|
Kural
|
Bir serinin değeri (toplamı), kısmî toplamlar dizisinin limitine eşittir.
|
Tanım
|
Kısmî toplamlar dizisi yakınsak olan seriye yakınsak seri, kısmî toplamlar dizisi ıraksak olan seriye ıraksak seri denir.
 serisinin kısmî toplamlar dizisi (Sn) olsun.
1. (Sn) dizisi ıraksak ise serisi de ıraksaktır.
2. (Sn) dizisi yakınsak ise serisi de yakınsaktır.
|
Kural
|
1. serisi yakınsak ise lim(an) =0 dır.
2. lim(an) = 0 iken yakınsak olmayabilir.
3. lim(an) ¹ 0 iken ıraksaktır.
|
B. ARİTMETİK SERİLER
(an) dizisi bir aritmetik dizi ise,
serisine aritmetik seri denir.
Aritmetik serinin n. kismî toplamı:
C. GEOMETRİK SERİLER
(an) dizisi bir geometrik dizi ise,
serisine geometrik seri denir.
geometrik serisinin n. kismî toplamı:
Kural
|
geometrik serisinde;
|r| ³ 1 ise seri ıraksaktır.
|r| < 1 ise seri yakınsaktır.
Yakınsak ise, serinin toplamı:
|
