|
|
| |
Polinomlar özel tipte bazı fonksiyonlardır. Tek değişkenli n. dereceden bir polinomun genel şekli
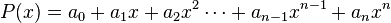
dir. Burada a0,...,an katsayılardır ve Reel sayı olmak zorundadır. Değişkenin üssü olan n ise bir Doğal sayıdır. Polinomda + ile ayırdığımız a0, a1x,..., anxn şeklindeki değişken, katsayı ve üs bileşimine terim denir. Polinomdaki en büyük üssüye polinomun dercesi denir. Örnek:
| |}
- P(x) = 3 + 5x4 + 7x5 + x13 derP(x)=13
- P(x) = 7x4 − 3x2 + 14x − 2 derP(X)=4
n. dereceden bir polinomun en cok n kökü vardır (kök, polinomun değerini sıfır yapan sayıdır, yani P(a) = 0 koşulunu sağlayan a sayılarına P'nin kökleri denir). Bir a sayısı P(x) polinomunun bir köküyse, (x-a) terimi P(x)'in bir çarpanıdır.
Örneğin:
- P(x) = x2 − 1 olsun.
P(1) = 0 koşulu sağlandığından
- P(x) = x2 − 1 = (x − 1)(x + 1) eşitliği yazılabilir.
Bu polinomun kökleri -1 ve +1'dir. Cebirin Temel Teoremine göre her polinomun en az bir kökü vardır. Bu kök her zaman reel sayı olmayabilir, bazen kökler karmaşık sayılardan oluşabilir.
Örneğin :
- P(x) = x2 + x + 1
polinomunun (reel sayılarda) kökü yoktur, reel çarpanlara ayrılmaz. Bu polinomun kökleri sanal sayılar olarak bulunabilir.
- P(x) = ax2 + bx + c
şeklinde bir polinomun kökleri
 ve 
formülleriyle verilir. Burada
- b2 − 4ac < 0
ise polinomun gerçel kökü yok demektir. Bu durumda kökler sanaldır.
3. ve 4. derece polinomların koklerini veren karışık formüller vardır. 5. ve üstü derecelerdeki polinomların köklerini verebilecek bir formül yoktur. Yani, yalnızca 4 işlem ve üs, kök alma işlemlerini kullanan bir formülün var olamayacağı 19. yüzyılda Niels Henrik Abel tarafından ispatlanmıştır.
- der[P(x)] = m, der[Q(x)] = n olmak üzere,
m > n ise, der[P(x)+/- Q(x)] = m
m = n ise, der[P(x)+/- Q(x)] < m ya da der[P(x) ± Q(x)] = m'dir.
- der[P(x)] = m, der[Q(x)] = n olmak üzere,
der[P(x) . Q(x)] = m+n
der[P(x) / Q(x)] = m-n 'dir.
******************************************************************************************************
ao, a1, a2 ........an R ve n N olmak üzere
P(x) = an xn + an–1xn–1 + an–2xn–2 + ..... + a1x + ao biçimindeki çok terimlilere polinom denir.
3x3 + 2x2 – 5x + 3 bir polinomdur.
2 x4 – 3x2 – 6x + 3 bir polinomdur.
–3 x2 + 5x – 1 polinom değildir.
x3 – x–2 + x + 4 polinom değildir.
Bir polinomun derecesi en büyük dereceli terimin derecesidir.
Örneğin x3 – 3x2 + 4 üçüncü dereceden bir polinomdur.
P(x,y) = x5 + x2y2+ x4y2 + y3 – x gibi iki bilinmeyenlerin üsleri toplamıdır.
Örneğin yukarıdaki polinomda x4y2 teriminin derecesi 4+2 = 6 dır.
Bir P(x) polinomunun derecesini d ( P(x) ) biçiminde göstereceğiz.
Örneğin, x4 – 2x3 + 5x2 + x + 3 ise
d ( P(x) ) = 4 dür.
İki polinomun eşitliği (denkliği):
O iki polinomun derecelerinin aynı ve aynı dereceden terimlerinin katsayılarının eşitliği ile tanımlanır.
P(x) = ax3 + bx2 + cx + d
Q(x) = 2x2 – 3x + 4
iken,
P(x) = Q(x) ise:
ax3 + bx2 + cx + d = 2x2 – 3x + 4 den
a = 0, b = 2, c = –2 ve d = 9 bulunur.
POLİNOMLARDA TOPLAMA – ÇIKARMA
Toplama ve çıkarma aynı dereceden terimlerin toplama veya çıkarılması ile yapılır.
ÖRNEK :
P(x) = 2x3 + 3x2 – 5x + 4
Q(x) = 5x2 + 6x2 + 5
ise P(x) + Q(x) ve P(x) – Q(x) ifadelerinin eşitlerini bulunuz?
Çözüm :
P(x)+Q(x) = (2x3 + 3x2 –5x + 4) + 5x3+6x2+5
= 7x3 + 9x2 – 5x + 9
P(x)-Q(x) = (2x3 = 3x2 – 5x+4) – (5x3+6x2+ 5)
= 2x3 + 3x2 – 5x + 4 – 5x3 – 6x2 – 5
= –3x3 – 3x2 – 5x – 1
POLİNOMLARDA ÇARPMA
a) Tek terimli bir polinomun çok terimli bir polinomla çarpımını yapmak için çarpmanın toplama üzerine dağılma özelliği uygulanır.
Örneğin;
3x2(2x3 – 3x2 + 5x – 3) = 6x5 – 9x4 + 15x3 – 9x2 dir.
b) Çok terimlilerin çarpımında, birinci polinomun her terimi ikinci polinomun her terimi ile ayrı ayrı çarpılır. Bunların toplamı alınır.
Polinomların çarpımında, çarpımın derecesi, çarpanların dereceleri toplamına eşittir.
d(P(x) . Q(x)) = d(P(x) + d(Q(x) ) dır.
ÖRNEK :
P(x) = x2 – 2x + 1
Q(x) = x3 – 3x2 ise P(x). Q(x) = ?
Çözüm :
P(x) . Q(x) = (x2 – 2x + 1) (x3 – 3x2)
= x5 – 3x4 – 2x4 + 6x3 + x3– 3x2
= x5 – 5x4 = 7x3 , 3x2
ÖRNEK :
P(x) = x3 – 7x
Q(x) = x3 + 7x ise P(x) . Q(x) = ?
Çözüm :
P(x) . Q(x) = (x3 – 7x) . (x3 + 7x)
= x6 + 7x4 – 7x4 – 49x2
= x6 – 49x2
ÖRNEK :
P(x) = x12 + x3 + x2 + 2x + 1
Q(x) = xn + xn–1 + x
( P(x) . Q(x) ) ın derecesi 15 ise n kaçtır?
Çözüm :
d ( P(x) . Q(x) = d ( P(x) ) + d(Q(x)) olduğu için
15 = 12 + n n = 3 tür.
ÖRNEK :
polinomunun derecesi kaçtır?
Çözüm :
n + 24 ve 8n doğal sayı olmalıdır. Buradan n = 2 ise
2+24 = 1 ve 82 = 4 bulunur.
O halde polinom
P(x) = 3x + 2x4 = 3x2 + 4 biçimindedir. Azalan kuvvetlere göre sıralanırsa
P(x) = 2x4 + 3x2 = 3x + 4 dür.
P(x) in derecesi 4 olarak bulunur.
Polinomlarda bazı özel çarpımlar vardır. Bunlara özdeşlikler de denir. Bu çarpımları ezbere bilmek gerekir. Bunları tersinden kullanarak çarpanlara ayırmaları yaparız.
ÖZDEŞLİKLER :
1) (x – y) (x + y) = x2 – y2
2) (x – y) (x2 + xy + y + y2
3) (x – y) (x3 + x2y + xy2 + y4) = x4 – y4
4) Genel olarak
(x–y) (xn–1 + xn–2y + xn–2 y2 +...+ xyn–2 + yn–1)=xn–yn dir.
5) x + y ≠ 0 koşulu ile
(x + y)0 = 1
(x + y)1 = x + y
(x + y)2 = x2 + 2xy + y2
(iki terimli toplamın karesi: birincinin karesi + birinci ile ikincinin çarpımının iki katı + ikincinin karesidir.)
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(İki terimin toplamının küpünü siz yukarıdaki gibi ifade edin.
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4 dür.
Terimlerde xin üzeri bir azalırken y nin üzeri bir artarak sıra ile yazıldığına dikkat ediniz. Kat sayıları paskal üçgeninden bulunur.
Paskal üçgeni:
Örneğin (x + y)5 in açılımı istense 5. derece (6. sıra) karşısında bulunan sayılar sıra ile katsayı olarak alınırlar ve,
(x+y)5 = x5 + 5xy4 + 10x3Y2 + 10x2y3 = 5xy4 + y5 olarak bulunur.
6) x – y ≠ 0 için
(x – y)0 = 1
(x – y)1 = x – y
(x – y)2 = x2 – 2xy + y2
(x – y)3 = x3 – 3x2y + 3xy2 – y3
*************************************************************************
POLİNOMLAR
A. POLİNOMLAR
 olmak üzere,
P(x) = a0 + a1 × x + a2 × x2 + ... + an × xn
biçimindeki ifadelere x değişkenine göre, düzenlenmiş reel kat sayılı polinom (çok terimli) denir.
Burada, a0, a1, a2, ... an reel sayılarına polinomun kat sayıları,
a0, a1 × x , a2 × x2 , ... , an × xn ifadelerine polinomun terimleri denir.
an × xn terimindeki an sayısına terimin kat sayısı, x in kuvveti olan
n sayısına terimin derecesi denir.
Derecesi en büyük olan terimin derecesine polinomun derecesi denir ve der[P(x)] ile gösterilir. Derecesi en büyük olan terimin kat sayısına ise polinomun baş kat sayısı denir.
Polinomlar kat sayılarına göre adlandırılırlar. Kat sayıları reel sayı olan polinomlara reel kat sayılı polinom, kat sayıları rasyonel sayı olan polinomlara rasyonel kat sayılı polinom, kat sayıları tam sayı olan polinomlara tam kat sayılı polinom denir.
Tanım
 olmak üzere, P(x) = c biçimindeki polinomlara, sabit polinom denir. Sabit polinomun derecesi 0 (sıfır) dır.
Tanım
P(x) = 0 biçimindeki polinoma, sıfır polinomu denir. Sıfır polinomunun derecesi tanımsızdır.
Polinomların Eşitliği
Aynı dereceli terimlerinin kat sayıları eşit olan polinomlar eşittir.
B. POLİNOMLARDA İŞLEMLER
1. Toplama İşlemi
İki polinom toplanırken; dereceleri aynı olan terimlerin kat sayıları kendi aralarında toplanır, sonuç o terimin kat sayısı olarak yazılır.
2. Çıkarma İşlemi
P(x) – Q(x) = P(x) + [–Q(x)]
olduğu için, P(x) polinomundan Q(x) polinomunu çıkarmak, P(x) ile
–Q(x) i toplamaktır. Bunun için çıkarma işlemini, çıkarılacak polinomun işaretini değiştirip toplama yapmak biçiminde ele alabiliriz.
3. Çarpma İşlemi
İki polinomun çarpımı; polinomlardan birinin her teriminin diğer polinomun her bir terimi ile ayrı ayrı çarpımlarından elde edilen terimler toplamınarak yapılır.
4. Bölme İşleminin Yapılışı
Polinomlarda bölme işlemi, sayılarda bölme işlemine benzer şekilde yapılır. Bunun için sırasıyla aşağıdaki işlemler yapılır:
1) Bölünen ve bölen polinomlar x değişkeninin azalan kuvvetlerine göre sıralanır.
2) Bölünen polinomun soldan ilk terimi, bölen polinomun soldan ilk terimine bölünür. Çıkan sonuç, bölümün ilk terimi olarak yazılır.
3) Bulunan bu bölüm, bölen polinomun bütün terimleri ile çarpılarak, aynı dereceli terimler alt alta gelecek şekilde bölünen polinomun altına yazılır.
4) Bölünenin altına yazılan çarpım polinomu, bölünen polinomdan çıkarılır.
5) Yukarıdaki işlemlere, kalan polinomun derecesi, bölen polinomun derecesinden küçük oluncaya kadar devam edilir.
Tanım
m > n olmak üzere,
der[P(x)] = m ve der[Q(x)] = n olsun.
P(x) in Q(x) ile bölümünden elde edilen bölüm polinomu B(x) olsun.
Buna göre,
 der[P(x) + Q(x)] = m,
der[P(x) – Q(x)] = m,
der[P(x) × Q(x)] = m + n,
der[B(x)] = m – n,
der[[P(x)]k] = k × der[P(x)] = k × m,
der[[P(xk)]] = k × der[P(x)] = k × m dir.
C. P(x) İN x = k İÇİN DEĞERİ
P(x) = a0 + a1 × x + a2 × x2 + … + an × xn
polinomunun x = k için değeri,
P(k) = a0 + a1 × k + a2 × k2 + … +an × kn dir.
Kural
P(x) = a0 + a1 × x + a2 × x2 + … + an × xn
polinomunda x = 1 yazılırsa,
P(1) = a0 + a1 + a2 + ... + an olur.
Bu durumda P(1) in değeri P(x) polinomunun kat sayıları toplamıdır.
Sonuç
Herhangi bir polinomda x yerine 1 yazılırsa, o polinomun kat sayıları toplamı bulunur.
Örneğin, P(x + 7) polinomunun kat sayıları toplamı,
P(1 + 7) = P(8) dir.
Kural
P(x) = a0 + a1 × x + a2 × x2 + … + an × xn
polinomunda x = 0 yazılırsa,
P(0) = a0 olur.
Bu durumda P(0) ın değeri P(x) polinomunun sabit terimidir.
Sonuç
Herhangi bir polinomda x yerine 0 yazılırsa, o polinomun sabit (x ten bağımsız) terimi bulunur.
Örneğin, P(2x + 3) polinomunun sabit terimi,
P(0 + 3) = P(3) tür.
D. P(x) İN (ax + b) İLE BÖLÜNMESİYLE ELDE EDİLEN KALAN
P(x) in ax + b ile bölünmesiyle elde edilen bölüm B(x), kalan K olsun. Buna göre,
Yani; P(x) polinomunun ax + b ile bölünmesiyle elde edilen kalanı bulmak için, ax + b = 0 denkleminin kökü olan  için P(x) polinomunun değeri olan  hesaplanır.
Sonuç
P(x) polinomunun x – a ile bölümünden kalan P(a) dır.
P(x + b) polinomunun x – a ile bölümünden kalan
P(a + b) dir.
P(3x + b) polinomunun x – a ile bölümünden kalan
P(3 × a + b) dir.
E. P(x) İN xn + a İLE BÖLÜMÜNDEN KALAN
Kural
Derecesi n den büyük olan bir polinomun
xn + a ile bölümünden kalanı bulmak için, xn yerine –a yazılır.
(xn + a = 0 ise, xn = –a)
F. P(x) İN (x – a) × (x – b) ÇARPIMI İLE BÖLÜNMESİ
Kural
1) P(x) polinomu (x – a) × (x – b) çarpımı ile tam olarak bölünebiliyorsa x – a ve x – b çarpanları ile de ayrı ayrı tam olarak bölünür.
2) x – a ve x – b aralarında asal polinomlar olmak üzere;
P(x), bu polinomlara ayrı ayrı tam olarak bölünebiliyorsa, (x – a) × (x – b) çarpımı ile de tam olarak bölünür.
G. P(x) İN (a × x + b)2 İLE BÖLÜNEBİLMESİ
P(x) polinomu (ax + b)2 ile tam bölünebiliyorsa,
P(x) polinomu ve P'(x) polinomu ax + b ye tam olarak bölünür.
(P'(x), P(x) in türevidir.)
Buna göre, P(x) polinomu (ax + b)2 ile tam bölünebiliyorsa,
Konuyla alakalı linkler:
-Polinomlar videolu konu anlatımı>>
|
|
|
|
|
|
