15.1 türev from detay hoca on Vimeo.

15.2 türev from detay hoca on Vimeo.

TÜREV FORMÜLLERİ

Tanım

Türev Kuralları

x 'in Kuvveti

Üstel / Logaritmik

Trigonometrik

Ters Trigonometrik

Hiperbolik

Birinci tanTürevin tanımı ( nedir) 

Dikkat: Konuya başlamadan önce mutlaka Prof. Dr. Ali Nesin'in Türev hakkında yazısını okuyunuz.
f : A → R, y = f(x) fonksiyonu a ∈ A’da sürekli olmak üzere, limiti bir reel sayıya eşitse; bu değere f(x) fonksiyonunun x = a noktasındaki türevi denir. y = f(x) fonksiyonunun x = a noktasındaki türevi denir.Burada f(x) fonksiyonunun x = a noktasındaki türevi,



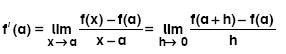
dır.

Alltaki Konu anlatımı videolarında
* Türevin tanımını ve gösterilişini öğrenecek,
* Bir noktada türev almayı öğrenecek,
* Sağdan ve soldan türevleri kavrayacak,
* Türev kurallarını kavrayıp, örnek çözecek,
* Ters ve kapalı fonksiyonların türevlerini almayı öğrenecek,
* Bileşke fonksiyonun türevini almayı öğrenecek,
* Parametrik fonksiyonlarda türev almayı öğrenecek
* Ardışık türev almayı öğrenecek,
* Trigonometrik fonksiyonların türevlerini almayı öğrenecek,
* Ters trigonometrik fonksiyonların türevlerini almayı öğrenecek,
* Logaritma ve üstel fonksiyonların türevlerini almayı öğrenecek,
* L’ Hospital kuralını kavrayıp limit problemlerinde 0/0 , ∞/∞ belirsizliğindeki durumlar için türevi kullanacak,
* Teğetin eğimini ve normalin denklemini türev yardımıyla bulmayı öğrenecek,
* Hız ve ivme problemlerinde türevden yararlanmayı öğrenecek,
* Özel tanımlı fonksiyonların türevlerini almayı öğrenecek,
* Her türevlenebilen fonksiyon sürekli mi yoksa aksi de doğru mu sorularının cevabını bulacak,
* Ekstremum değerin ne olduğunu öğrenecek, fonksiyonların ekstremum değerini bulacak,
* Fonksiyonun yerel maksimum veyerel minimum noktaları bulmayı öğrenecek,
* Rolle ve ortalama değer teoreminin türevde ne işe yaradığını öğrenip, bu teoremler sayesinde ilgili soruları çözmeyi öğrenecek,
* İkinci türevin geometrik anlamını kavrayacak, niçin ikinci türev gerekli sorusunun cevabını bulacak,
* Maximum ve minimum problemleri için türevin gerekliliğini anlayacak,
* Fonksiyonların asimptotlarını bulmayı öğrenecek,
* Çeşitli fonksiyonların grafik çizimlerini yapabileceksiniz.